Dans mon article précédent j’ai calculé la polaire des vitesse de ma Gin Glider Camino XS chargée au sommet de sa fourchette. On peut utiliser les mêmes mesures pour déterminer la vitesse de vol préscrite par la théorie de McCready. Le principe est bien décrit par cet extrait de wikipedia:
En vol de plaine (le contexte est différent en région montagneuses), les ascendances sont localisées dans l’espace et dans le temps, elles alternent avec des zones de subsidences, généralement plus vastes. En présence de vent, le planeur voit sa vitesse par rapport au sol varier en fonction de sa route. La tactique, pour parvenir à couvrir la plus grande distance possible en opérant à la plus grande vitesse possible, consiste à utiliser une vitesse optimale, c’est-à dire adaptée aux conditions rencontrées pour obtenir la meilleure performance.
En appliquant cette théorie à mon parapente on obtient le graphique suivant:
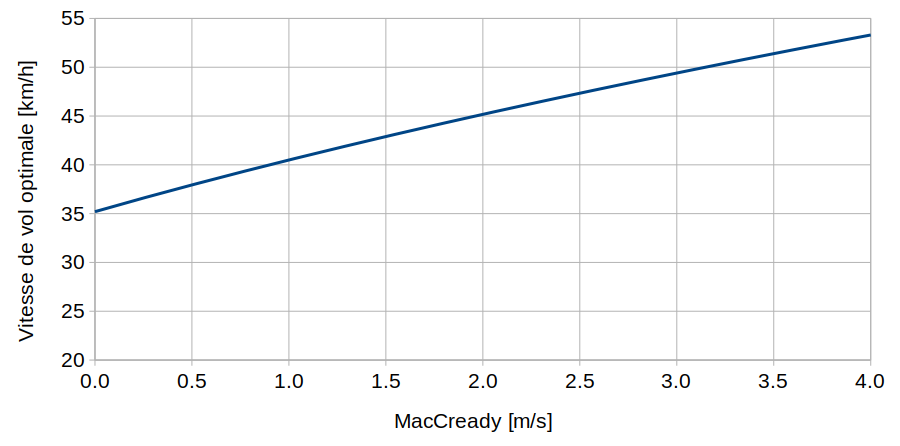
L’axe vertical correspond à la vitesse de vol optimale en km/h entre deux thermiques. L’axe horitontal correspond au paramètre McReady.
Dans un cas idéal où il n’y a ni vent, ni ascandence, ni subsidence durant la transition, il est le taux de montée que l’on attend dans le prochain thermique.
Si on convertit la vitesse de vol en le taux d’accélérateur qu’il faut pour atteidndre cette vitesse on obtient la figure suivante:
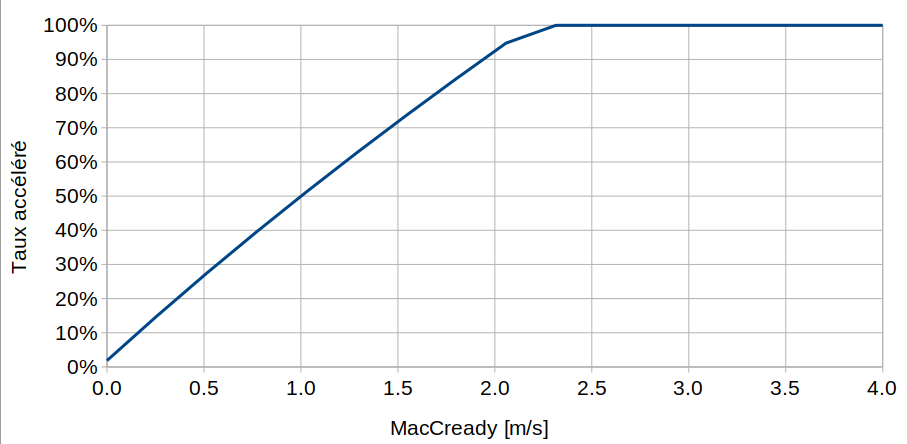
Donc dès que le taux de montée attendu est de au moins 2.5 m/s, il faut accélérer à fond. Bien entendu ceci est valabe que si on atteint le thermique suivant… Une autre chose à considérer est que le taux de montée du thermique doit être moyenné sur tout le thermique, y compris les premiers tours où on cherche le centre. Cette valeur est largement inférieure au maximum du taux de montée que l’on évoque souvent.

Commentaires récents