Introduction

Je viens de m’inscrire à la compétition de marche et vol Jura Hike & Fly et je me suis demandé si il y avait une théorie similaire à celle du speed to fly pour optimiser sa tactique. Ne trouvant rien, j’ai décidé d’essayer de le faire moi-même.

Mise en équation du problème

Imaginons le cas suivant. Nous sommes en plaine tôt le matin avec le parapente sur le dos et nous voulons aller le plus vite possible dans la direction de la prochaine balise. ll n’y a pas de thermique ni de vent. Il se trouve que l’on est au pied d’ une colline avec un décollage au sommet. Deux options s’offrent à nous pour continuer d’avancer:

• rester en plaine et marcher à plat (option hike).
• monter sur la colline puis voler jusqu’en plaine (option hike & fly).

Les deux options sont décrites dans la figure ci-dessous pour une colline d’une hauteur h au dessus de la plaine et une distance d à parcourir.

Quelle option est la plus rapide? Pour répondre à cette question on peut mettre le problème en équation et calculer le temps nécessaire pour chacune des variantes.

Soit:

\( V_v\) : vitesse verticale en montée à pied

\( V_p\) : vitesse à pied au plat

\( V_a\) : vitesse horizontale en vol

\( t_p\) : temps nécessaire pour plier et ranger le parapente

\( t_{dp}\) : temps nécessaire pour déplier le parapente et décoller

\( h\) : dénivelé de la montée à pied

\( d\) : distance horizontale en vol

\( f\) : finesse en vol

\( t_{h}\) : temps de déplacement en mode hike

\( t_{h \& f}\) : temps de déplacement en mode hike & fliy

Et la définition de la finesse: \( f= \frac{d}{h}\)

Alors

Le temps du parcours de l’option hike est: \( t_{h} = \frac{d}{V_p} \)

Le temps du parcours de l’option hike & fly est : \( t_{h \& f} = \frac{h}{V_v}+ t_{dp} + \frac{d}{V_a}+ t_p\)

Application des équations

En fixant les paramètres on peut maintenant calculer le temps de chaque option et ce faisant de déterminer laquelle est la plus rapide.

Par exemple:

\( V_v = 700\) mètres par heure

\( V_p = 5\) kilomètres par heure

\( V_a=36\) kilomètres par heure

\( t_p=10\) minutes

\( t_{dp}=10\) minutes

\( h=700\) : mètres

\( f=10\)

ce qui entraîne:

\( t_h = 1h24\)

\( t_{h\&f} = 1h31 \)

Et donc dans le cas présent pour être le plus rapide possible il faut mieux marcher en plaine.

Si on change un peu les paramètres et que la hauteur de la colline est de 1500 m alors

\( t_h = 3h\)

\( t_{h\&f} = 2h54 \)

Et cette fois c’est l’option hike & fly qui est la plus rapide.

Hauteur minimale

On comprend que globalement plus la colline est haute, plus l’option hike & fly est avantageuse. A partir de quelle hauteur exactement il est plus rapide de monter et voler? Pour répondre à cela il faut encore un peu manipuler les équations.

On pose \( t_h = t_{h\&f} \) et on résout.

(1) \( h_{min} =\frac{t_{dp}+t_p}{\frac{f}{V_p}-\frac{1}{V_v}-\frac{f}{V_a}} \)

Si on reprend les paramètres définit plus haut on obtient:

\( h_{min} = 1135 \) mètres.

Donc si le dénivelé jusqu’au décollage est inférieur à 1135 m., il est plus rapide de marcher en plaine. Dans le cas contraire il faut déployer ses ailes!

Naturellement cette hauteur critique dépend des autres paramètres. Si on est plus rapide pour plier et déplier son parapente, alors on imagine bien qu’il est plus vite avantageux de voler. Grâce à l’équation (1) on peut déterminer cette dépendance:

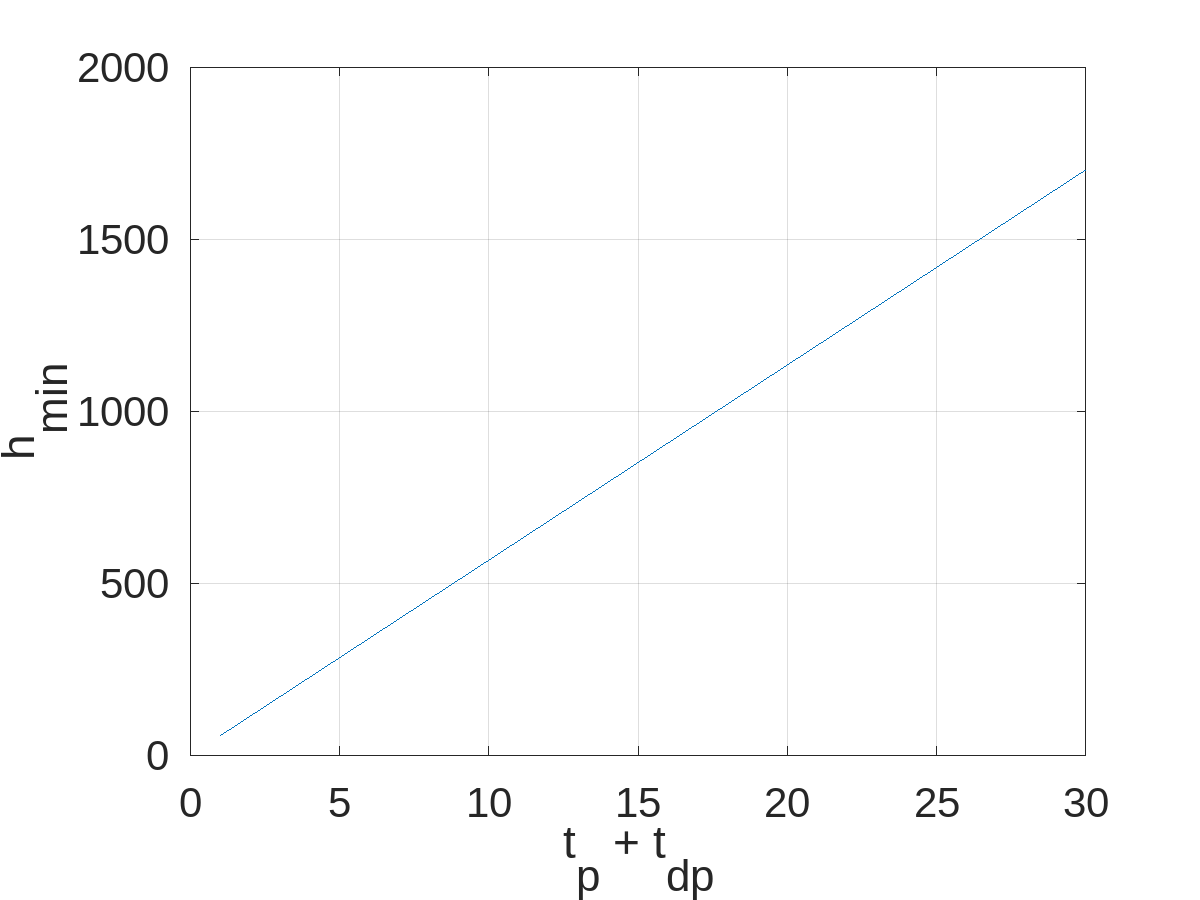
Par exemple si il faut 10 minutes pour déplier et plier son matériel, il faut que le décollage soit au moins 560 m plus haut que la plaine. Si on a besoin de 25 minutes, au moins 1400 m.

On peut aussi d’intéresser à dépendance de la hauteur minimal en fonction de la vitesse verticale.

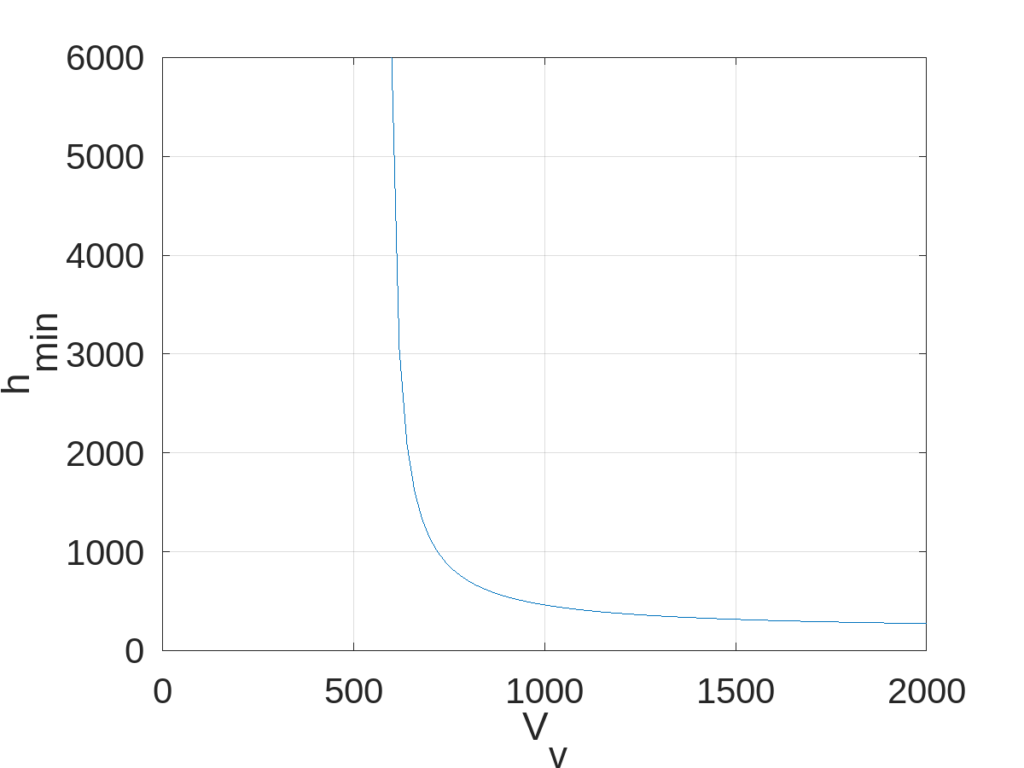
Comme on s’y attend plus la vitesse verticale est élevée, moins la hauteur du décollage à besoin d’être élevé. D’autre part on voit que si la vitesse verticale est inférieur à environ 600 m/h, la hauteur minimal n’est plus définie, ou en d’autres mots l’option hike est la meilleur. On peut d’ailleurs calculer précisément cette vitesse minimale:

\(V_{v_m} = \frac{1}{f(\frac{1}{V_p} – \frac{1}{V_a})}\)

Dans le cas présent \(V_{v_m} = \) 580 m/h

Un aspect que l’on a pas considéré jusqu’à maintenant est le fait que le parcours en plaine ne se fait pas sur un chemin rectiligne. Une façon d’en tenir compte est d’introduire un nouveau paramètres alpha définit comme suit:

\(\alpha = \frac{d_s}{d}\) où \(d_s\) est la longueur du chemin au sol.

En intégrant ce paramètre dans l’équation (1) on obtient:

(2) \( h_{min} =\frac{t_{dp}+t_p}{\frac{f\alpha}{V_p}-\frac{1}{V_v}-\frac{f}{V_a}} \)

et on peut alors calculer la dépendance de la hauteur minimale en fonction de alpha:

Conclusion

Nous avons mis en équation un cas idéalisé où on doit choisir entre deux options: marcher en plaine, ou monter sur une colline et planer jusqu’en plaine. Essentiellement pour que la variante hike & fly soit avantageuse il faut que la hauteur de la colline soit suffisante. Cette hauteur minimale dépend de nombreux facteur et en particulier de notre vitesse en montée à pied, du temps nécessaire pour plier et ranger sa voile, et du chemin à suivre en plaine. Grâces aux équations introduites Il est possible de décrire ces dépendance avec des courbes.

Cette mise en théorie est une premier essais et on peut encore beaucoup l’améliorer. Elle décrit un cas idéal et il est difficile de l’appliquer pour une cas pratique. D’autre part on pourrait aussi imaginer intégrer l’effort nécessaire pour chacune des des options.

Finalement les valeurs des paramètres choisis correspondent à mon expérience, et devrait donc être changé pour une autre personne.